Sorting algorithms

Sorting Algorithms are used to rearrange the given list or array in a certain order. In this post we are going to see working of some basic sorting algorithms like Bubble Sort, Insertion Sort, Quick Sort, Selection Sort and Merge Sort. We are going to implement these algorithms in JavaScript.

Bubble Sort

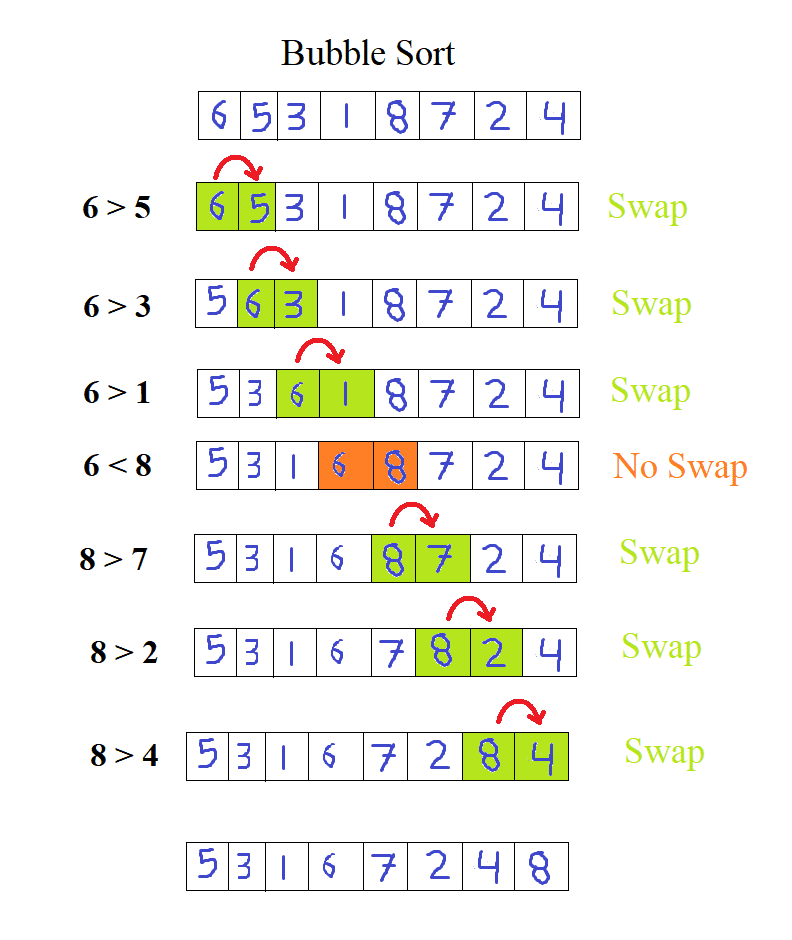
Bubble Sort is a simple sorting algorithm where the largest value bubble up to the top. It repeatedly steps through the array then compares adjacent pairs and swaps them if they are in the wrong order.

Steps involed in Bubble Sort:

1. We will start with the first element, compare with the next element of the array.
2. If the current element is greater than the next element then we will swap them.
3. If the current element is less than the next element, move to the next element. Repeat Step 1.

Pictorial Representation of how bubble sort will sort the given arrray.

function BubbleSort(list) {
  let temp;
  for (let i = 0; i < list.length; i++) {
    for (let j = 0; j < list.length - 1; j++) {
      if (list[j] > list[j + 1]) {
        // Swap Elements
        temp = list[j];
        list[j] = list[j + 1];
        list[j + 1] = temp;
      }
    }
  }
  return list;
}

BubbleSort([29, 10, 14, 30, 37, 19, 18]);
}

Selection Sort

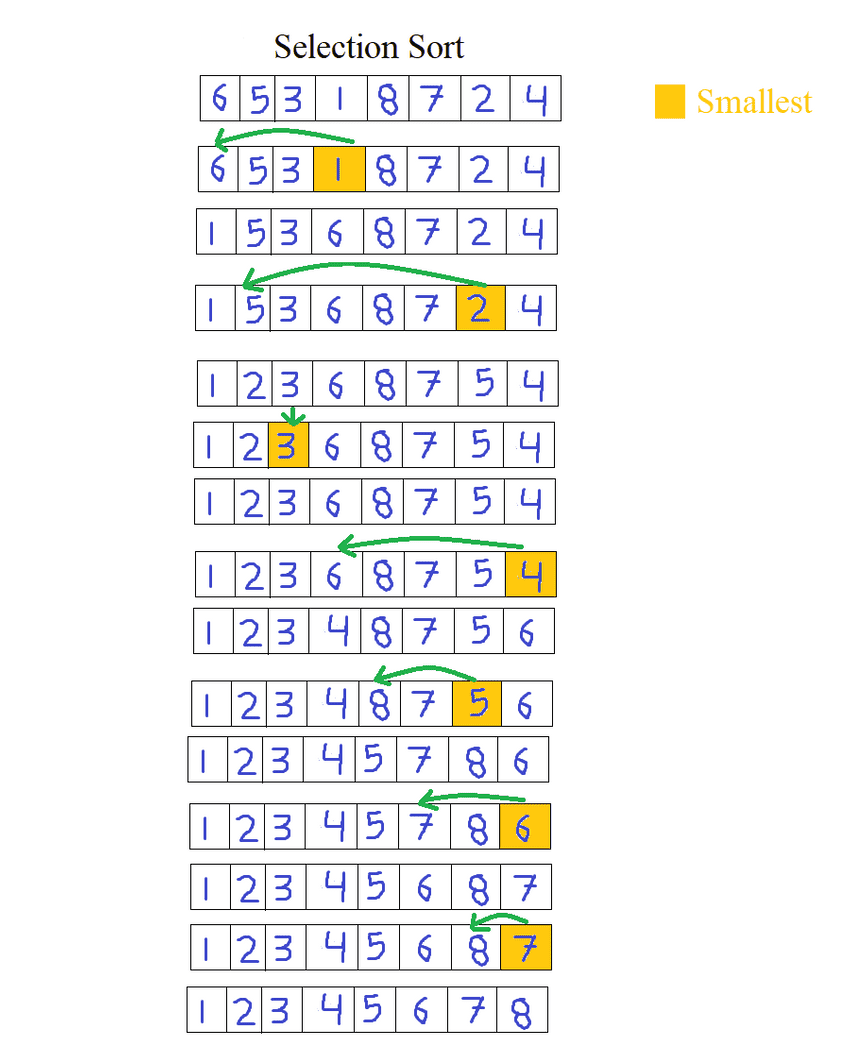
Selection sort is a simple algorithm where it divides the list into two sublists sorted and unsorted then repeatedly finding the smallest element and push or put it in on the beginning of the sorted array.

Steps involed in Selection Sort:

1. First will assume the first element is the smallest so that we can use it to compare and find the smallest element in the given array then we will swap it with the first element.
2. We then move to the second position and will look for the next smallest element in the remaining array or sub-list then we will replace that element in the second position.
3. We will repeatedly move to the next position and find the smallest after that we will replace the smallest element in the next position. until the array is completely sorted.

Pictorial Representation of how selection sort will sort the given arrray.

function SelectionSort(list) {
  for (let i = 0; i < list.length; i++) {
    // Assuming First Element is Lowest
    let lowest = i

    for (let j = i + 1; j < list.length; j++) {
      if (list[j] < list[lowest]) {
        // Find the smallest
        lowest = j
      }
    }
    // replacing smallest element in the respective position
    let temp = list[i]
    list[i] = list[lowest]
    list[lowest] = temp
  }
  return list
}

SelectionSort([29, 10, 14, 30, 37, 19, 18])

Insertion Sort

Insertion Sort is also a comparison based algorithm like selection sort and bubble sort. Insertion Sort maintains two sublists sorted and unsorted. it removes one element from the input list and finds its location in the sorted list and inserts it here. It repeats until no element remains in the input list.

Steps involed in Insertion Sort:

1. If it is the first element, it is already sorted.
2. Pick the next element.
3. Compare with all the elements in sorted sub-list.
4. Shift all the the elements in sorted sub-list that is greater than the value to be sorted.
5. Insert the value.
6. Repeat until list is sorted.

Pictorial Representation of how insertion sort will sort the given arrray.

function InsertionSort(array) {
  // Starting the loop from second position
  for (var i = 1; i < array.length; i++) {
    let nextValue = array[i]
    j = i - 1

    // check if previous no. is larger than value to be inserted
    while (j >= 0 && array[j] > nextValue) {
      array[j + 1] = array[j]
      j--
    }
    // insert the number at current position
    array[j + 1] = nextValue
  }
  return array
}
InsertionSort([29, 10, 14, 30, 37, 19, 18])

Merge Sort

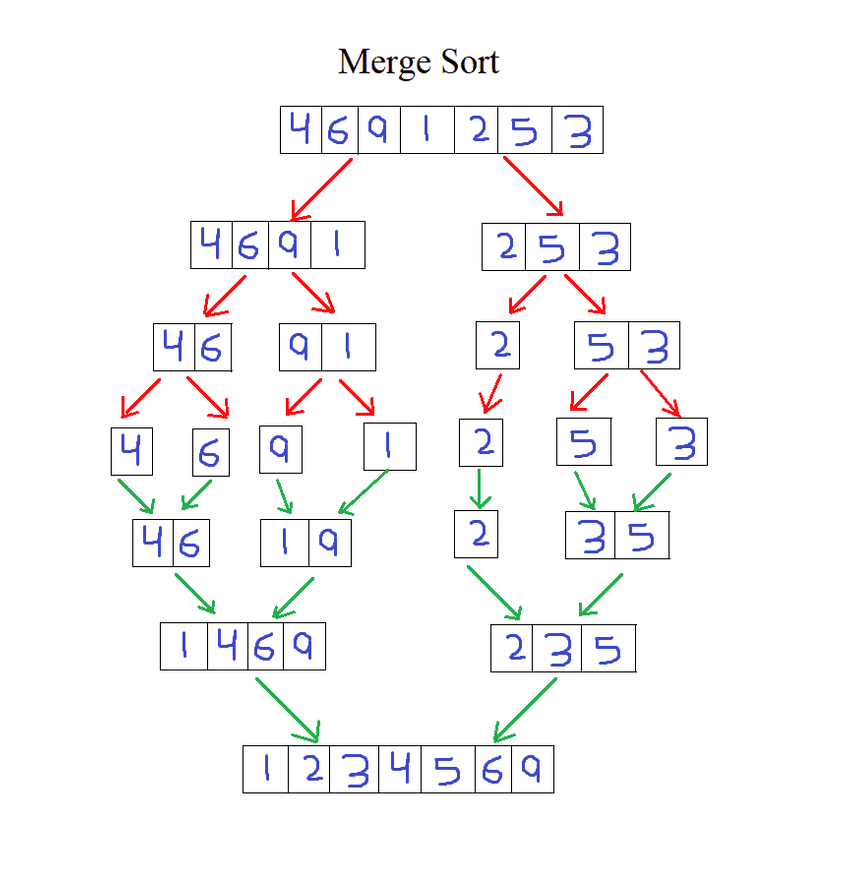
Merge Sort is an efficient sorting algorithm also it is a divide and conqueror algorithm where it divides the input list into two halves and then combines them in a sorted manner.

Steps involed in Merge Sort:

1. If it is only one element in the array it is already sorted, return.
2. Divide the array recursively into two halves until it can no more be divided.
3. Merge the smaller array into new array in sorted order then return that sorted array.

Pictorial Representation of how merge sort will sort the given arrray.

// Merging two arrays
function merge(array1, array2) {
  let results = [],
    j = 0,
    i = 0

  // Sorting and Pushing in results array
  while (i < array1.length && j < array2.length) {
    if (array2[j] > array1[i]) {
      results.push(array1[i])
      i++
    } else {
      results.push(array2[j])
      j++
    }
  }

  // Pushing Remaing elements from array1
  while (i < array1.length) {
    results.push(array1[i])
    i++
  }

  // Pushing Remaing elements from array2
  while (j < array2.length) {
    results.push(array2[j])
    j++
  }
  return results
}

// Recrusive Merge Sort
function MergeSort(array) {
  // base case to return arrayay
  if (array.length <= 1) return array

  // Dividing the Array in two halves
  let mid = Math.floor(array.length / 2)

  // Sort first and second halves
  let left = MergeSort(array.slice(0, mid))
  let right = MergeSort(array.slice(mid))

  return merge(left, right)
}

MergeSort([29, 10, 14, 30, 37, 14, 18])

Quick Sort

Quick Sort is also a divide and conqueror algorithm like Merge Sort. Quicksort first divides a large array into two smaller sub-arrays: the low elements and the high elements. Quicksort can then recursively sort the sub-arrays.

Steps involed in Merge Sort:

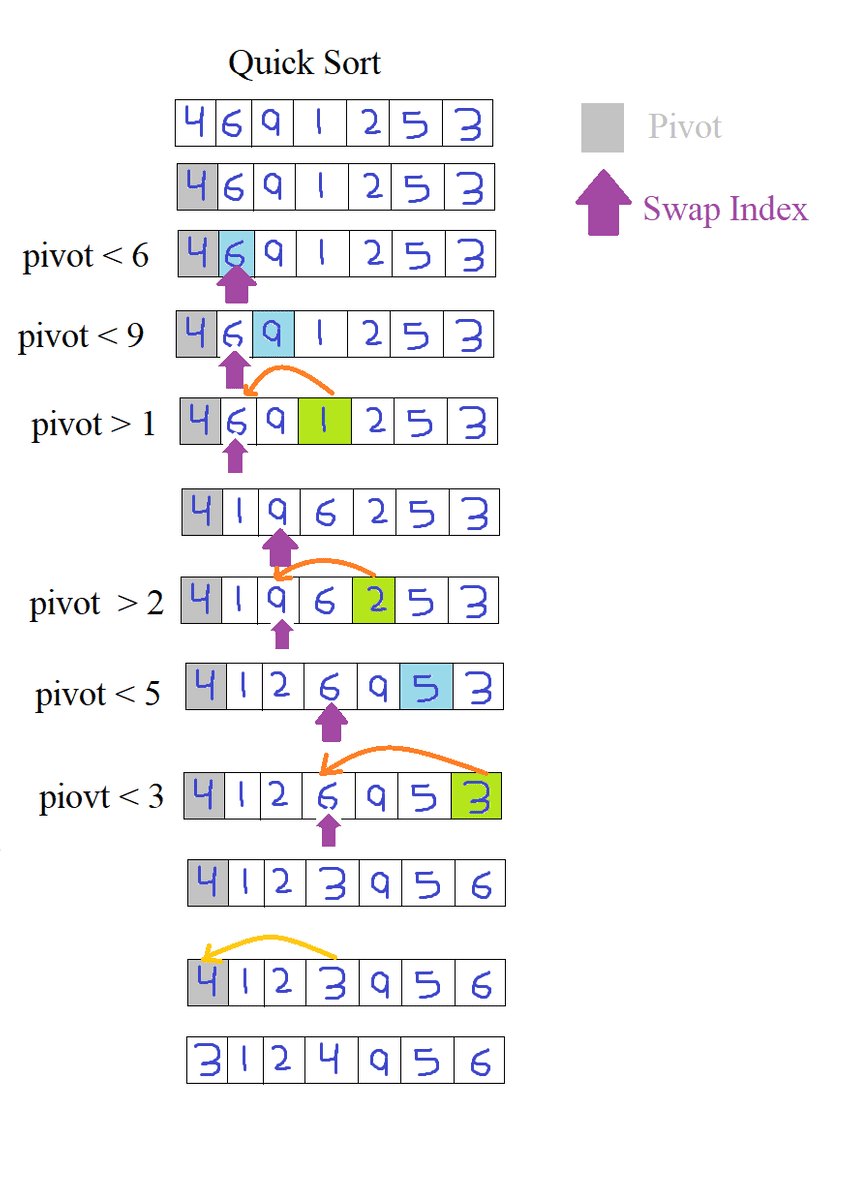
1. Find a “pivot” item in the array. we are considering first element.
2. Start a pointer (the left pointer) at the first item in the array.
3. Start a pointer (the right pointer) at the last item in the array.
4. While the value at the left pointer in the array is less than the pivot value, move the left pointer to the right (add 1). Continue until the value at the left pointer is greater than or equal to the pivot value.
5. While the value at the right pointer in the array is greater than the pivot value, move the right pointer to the left (subtract 1). Continue until the value at the right pointer is less than or equal to the pivot value.
6. If the left pointer is less than or equal to the right pointer, then swap the values at these locations in the array.
7. Move the left pointer to the right by one and the right pointer to the left by one.
8. If the left pointer and right pointer don’t meet, go to step 1.

Pictorial Representation of how quick sort will sort the given arrray.

function pivot(arr, start = 0, end = arr.length - 1) {
  const swap = (arr, idx1, idx2) => {
    ;[arr[idx1], arr[idx2]] = [arr[idx2], arr[idx1]]
  }

  // We are assuming the pivot is always the first element
  let pivot = arr[start]
  let swapIdx = start

  for (let i = start + 1; i <= end; i++) {
    if (pivot > arr[i]) {
      swapIdx++
      swap(arr, swapIdx, i)
    }
  }

  // Swap the pivot from the start the swapPoint
  swap(arr, start, swapIdx)
  return swapIdx
}

function QuickSort(arr, left = 0, right = arr.length - 1) {
  if (left < right) {
    let pivotIndex = pivot(arr, left, right)
    //left
    QuickSort(arr, left, pivotIndex - 1)
    //right
    QuickSort(arr, pivotIndex + 1, right)
  }
  return arr
}

QuickSort([4, 6, 9, 1, 2, 5, 3])

Consclusion

This article should have given you a good introduction how sorting algorithms work and how you can implement them in JavaScript.

The above implementation of all sorting algorithms provides you a basic understanding. They are not perfectly implemented or optimized.